해당 글은 CS182: Deep Learning의 강의를 정리한 글입니다. 여기서 사용된 슬라이드 이미지의 권리는 강의 원작자에게 있습니다.
Linear Regression
이전 lecture에서는 데이터를 Classification(분류)하는 문제를 다루었습니다. 하지만 머신러닝이 예측할 수 있는 데이터는 범주형 데이터만 있는게 아닙니다. 이번에는 범주형 데이터가 아니라 연속형 데이터를 예측하는 Regression 문제를 다뤄보겠습니다.

Model 정하기
Classification에서 골랐던 모델은 어떤 라벨인지 하나만 고르지 않고 각 라벨별 확률로 예측했습니다. 그렇기에 Regression에서도 특정한 값 하나가 아니라 확률로 예측할 것 입니다. Classification 모델은 각 라벨별 확률, 또는 확률 밀도를 예측했습니다. 그렇기에 Regression은 확률 분포를 예측합니다. 확률 분포를 예측한다면 연속형 데이터를 확률로 표현할 수 있습니다.
그렇다면 모델이 예측할 확률 분포는 어떤 것이 좋을까요? 여기서는 가장 보편적인 정규분포(Normal distribution)을 사용할 것입니다.
$$
p_\theta(y|x)=\mathcal{N}(f_\theta(x),\Sigma_\theta(x))
$$
Loss function 정하기
Loss function은 우리가 이전 lecture에서 본 NLL(Negative Likelihood-Loss)를 사용할 것입니다. 하지만 이전에는 $\log p_\theta(y_i|x_i)$를 바로 구할 수 있었지만, 이번에는 계산이 좀 필요합니다.
$$
\log p_\theta(y|x)=-\frac{1}{2}(f_\theta(x)-y)\Sigma_\theta(x)^{-1}(f_\theta(x)-y)-\frac{1}{2}\log|\Sigma_\theta(x)|+\mathrm{const}
$$
꽤나 복잡한 수식이 나왔습니다. 하지만 걱정할 필요가 없습니다. 여기서 $\Sigma_\theta(x)$는 벡터 $x$에서 변수 끼리의 공분산을 나타냅니다. 하지만 우리는 데이터셋을 수집할 때 데이터가 I.I.D.임을 가정했습니다. 다시 말하자면, $x$에서 변수끼리는 독립적입니다. 그렇기 때문에
$$
\Sigma_\theta(x)=I
$$
가 됩니다. 이를 바탕으로 $\log p_\theta(y|x)$을 다시 살펴보면,
$$
\begin{align}
\log p_\theta(y|x)
&=-\frac{1}{2}(f_\theta(x)-y)\Sigma_\theta(x)^{-1}(f_\theta(x)-y)-\frac{1}{2}\log|\Sigma_\theta(x)|+\mathrm{const}\\
&=-\frac{1}{2}||f_\theta(x)-y||^2+\mathrm{const},\ \mathrm{if}\ \Sigma_\theta(x)=I
\end{align}
$$
이 됩니다. 여기서 상수값까지 구할 필요는 없으니 Loss function을 다음과 같이 정의하며 됩니다.
$$
\mathcal{L}(x,y,\theta)=-\frac12||f_\theta(x)-y||^2
$$
이 식은 통계학을 공부하면 많이 보이는 식입니다. 보통 이 식을 Mean Squared Error(MSE) 라고 부릅니다. 여기서 Loss function을 MSE로 정할 겁니다. 물론 이외에도 Regression 문제에 사용할 수 있는 Loss function도 여러가지가 있습니다. 하지만 여기서는 간단한 식을 가진 MSE을 가지고 모델이 가지는 오차를 살펴볼 것입니다.
다만 여기서 주의할 점이 있습니다. 여기서 우리가 세운 식은 어디까지나 데이터가 I.I.D.를 만족한다는 가정하에 세워졌습니다. 실제로 데이터를 수집할 때 I.I.D.를 만족하지 않은 상태로 학습시킨다면 우리가 정한 Loss function은 부적절할 수 있습니다. 그렇기 때문에 우리의 가정인 I.I.D.를 잊지 말아야 합니다.
Variance와 Bias
이전 시간에 우리는 Overfitting과 Underfitting을 배웠습니다. 두가지 상황 모두 모델을 학습시킬 때 피해야 할 상황입니다. 그렇다면 우리는 어떻게 Overfitting과 Underfitting을 피할 수 있을까요? 이를 알아보기 위해 우리는 먼저 모델의 학습 성능을 평가할 방법을 찾아볼 것입니다.
데이터셋에 따른 모델의 성능

모델 학습의 목적은 주어진 점에 최대한 가깝게, 정해진 모양의 그래프를 그리는 작업에 비유할 수 있습니다. 여기서 우리가 그릴 그래프의 모양은 모델이 되고 주어진 점은 학습 데이터셋이 됩니다.
만약 우리가 그려야할 그래프가 고차함수이고, 주어진 점이 적으면 어떻게 될까요? 그렇다면 우리는 다양한 그래프를 그릴 수 있습니다. 고차함수인 만큼 곡선을 원하는 대로 집어넣을 수 있고 꼭 지나가야할 몇개의 점만 지나가면 됩니다. 그 외 나머지 부분은 우리가 원하는 만큼 그릴 수 있습니다. 하지만 진짜로 그렇게 마음대로 그래프를 그리게 된다면 실제 데이터 분포와 전체적으로 멀어진 그래프를 그리게 될 것입니다.
주어진 점은 무조건 지나가지만 실제 데이터 분포와 많이 멀어진 모습은 overfitting과 비슷한 양상을 보입니다. overfitting된 모델은 학습 데이터셋은 매우 정확하게 맞추지만 그 외 나머지 데이터는 오차가 큽니다. 그리고 같은 데이터셋을 학습시켜도 overfitting된 모델은 매우 다양하게 나올 수 있습니다.
이번에는 반대로 우리가 그려야할 선이 직선이라고 가정해봅시다. 그렇다면 우리는 언제나 주어진 점에 가깝게 선을 그을 수 있을까요? 실제 데이터 분포가 직선에 가깝다면 그렇겠지만 그렇지 않다면 어떻게 그리든 직선과 멀리 떨어진 점이 무조건 생길 겁니다. 그리고 최대한 모든 점과 멀어지지 않기 위해서 직선을 그리다보면 아무리 점을 많이 추가해도 직선이 크게 움직이지 않습니다.
이러한 모습은 underfitting과 유사합니다. 어떻게 그리든 주어진 점과의 거리가 멀듯이 underfitting된 모델은 loss 값이 꽤 큽니다. 그리고 학습 데이터셋을 추가한다고 해도 모델의 파라미터 값은 크게 달라지지 않습니다.
Bias-variance tradeoff
이처럼 모델이 학습할 데이터셋에 따라 모델의 성능에도 영향이 있다는 것을 알 수 있습니다. 그렇다면 이를 고려해 모델의 학습 성능을 살펴봅시다. 우리가 모델의 성능을 살펴볼 때 Loss 값을 계산했습니다. 그렇다면 좋은 모델일 때 어떤 데이터셋이 주어져도 loss 값이 낮아야 할 것입니다. 이를 수식으로 표현해봅시다.
$$
E_{\mathcal{D}\sim p(\mathcal{D})}[\mathcal{L}(\theta)]=E_{\mathcal{D}\sim p(\mathcal{D})}[||f_\mathcal{D}(x)-f(x)||^2]=\sum_\mathcal{D}p(\mathcal{D})||f_\mathcal{D}(x)-f(x)||^2
$$
여기서 $f_\mathcal{D}(x)$은 데이터셋 $\mathcal{D}$으로 학습시킨 모델의 예측, $f(x)$는 데이터의 실제 정답 $y$을 나타냅니다.
데이터셋 $\mathcal{D}$은 확률 분포 $p(\mathcal{D})$에 따라 추출되기 때문에 모델의 학습 성능을 모델 Loss의 기댓값으로 표현했습니다.
물론 해당 식의 값은 실제로 구할 수 없습니다. 모집단을 알 수도 없는데 가능한 모든 데이터셋 조합을 구할 수 없기 때문입니다. 하지만 이렇게 식으로 정리하는 이유는 모델 학습 성능의 성질을 찾아보기 위함입니다.
먼저 학습한 모델의 평균 $\bar{f}(x)$을 정의합니다.
$$
\bar{f}(x)=E_{\mathcal{D}\sim p(\mathcal{D})}[f_\mathcal{D}(x)]
$$
그리고 $\bar{f}(x)$을 가지고 위의 식을 변형해봅시다.
$$
\begin{align}
E_{\mathcal{D}\sim p(\mathcal{D})}[||f_\mathcal{D}(x)-f(x)||^2]
&=E_{\mathcal{D}\sim p(\mathcal{D})}[||f_\mathcal{D}(x)-\bar{f}(x)+\bar{f}(x)-f(x)||^2]\\
&=E_{\mathcal{D}\sim p(\mathcal{D})}[||f_\mathcal{D}(x)-\bar{f}(x)||^2]+E_{\mathcal{D}\sim p(\mathcal{D})}[||\bar{f}(x)-f(x)||^2]\\
&=\mathrm{Variance}+\mathrm{Bias}^2
\end{align}
$$
그러면 다음과 같이 두가지 Variance와 Bias로 나눌 수 있습니다. Variance란 학습한 모델이 모델 평균과 얼마나 차이나는지를 보여줍니다. Variance는 데이터셋에 따라 달라집니다. 그리고 Bias는 모델 평균이 실제 정답과 얼마나 차이나는지를 보여줍니다. Variance와는 달리 Bias는 데이터셋과 상관없이 항상 같은 값을 가지고 있습니다.
Variance와 Bias의 의미

우리는 Variance와 Bias를 통해 모델이 overfitting인지 underfitting인지 설명할 수 있습니다. 만약 모델의 Variance가 크다면 해당 모델은 overfitting될 가능성이 높습니다. Variance가 높다는 뜻은 그만큼 학습 데이터셋에 따라 모델간의 차이가 급격하다는 뜻이므로 학습한 모델의 Loss값이 클 확률이 그만큼 높습니다. 반대로 Bias 값이 크다면 이는 모델이 underfitting 하다는 의미입니다. Bias 값이 크다는 뜻은 학습 데이터셋에 상관없이 모델이 제대로 예측하지 못한다는 뜻입니다.
Bias와 Variance를 줄일 방법과 "tradeoff"
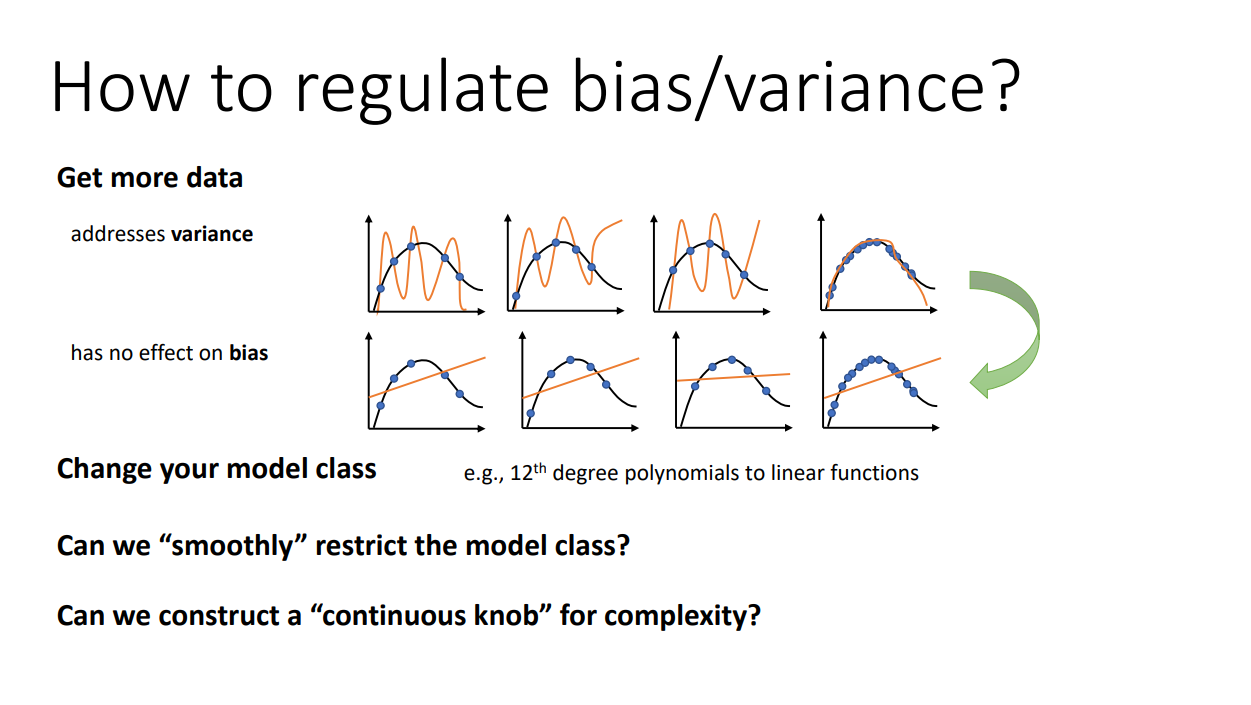
우리는 모델 자체가 데이터를 제대로 학습할 수 있는지 Bias와 Variance를 통해 알아볼 수 있습니다. 그렇다면 우리는 Bias와 Variance를 줄일 수 있다면 적합한 모델을 찾을 수 있을 겁니다.
가장 먼저 할 수 있는 방법은 학습 데이터셋을 키우는 것입니다. 학습할 데이터를 늘린다면 Variance를 줄일 수 있어 overfitting을 막을 수 있습니다. 다만 Bias는 데이터셋에 영향을 받지 않기 때문에 Bias가 큰 경우에는 효과적이지 않은 방법입니다.
Bias를 줄일 수 있는 좋은 방법은 더 복잡한 모델을 사용하는 것입니다. 모델이 복잡할 수록 실제 데이터 분포에 더 가깝게 그릴 수 있기 때문에 Bias를 줄일 수 있습니다. 하지만 모델이 복잡해지면 Variance가 증가합니다.
이처럼 Variance를 줄이면 Bias를 상승시킬 수 있고, Bias를 줄이면 Variance가 증가합니다. 이것이 Bias-Variance "Tradeoff"라고 불리는 이유입니다. 그렇기 때문에 Variance와 Bias의 합이 최소값을 가지도록 두가지 방법을 적당히 사용해야 합니다.
Regularization
모델을 복잡하게 만들수록 Bias를 줄일 수 있기 때문에 보통 모델의 성능을 향상시키기 위해 모델의 크기를 키웁니다. 하지만 위에서 봤듯이 복잡한 모델은 overfitting될 수 있습니다. 그렇다면 모델을 단순화하는 방법 말고 모델의 overfitting을 피할 방법은 없을까요?
Regularization (정규화)은 이처럼 모델의 overfitting을 피하는 방법들을 말합니다. Regularizaiton에 대한 접근법은 매우 다양합니다. 하지만 여기서는 Bayesian 접근법만 살펴보도록 하겠습니다.
Bayesian 접근법

Bayesian 방법으로 Regularization 문제를 표현해봅시다. 데이터셋 $\mathcal{D}$을 학습해 파라미터 $\theta$를 얻는 과정을 $p(\theta|\mathcal{D})$를 구하는 것이라고 표현할 수 있습니다. 그렇다면 $p(\theta|\mathcal{D})$는 어떻게 구할 수 있을까요? 우리는 Naive Bayes를 통해 다음과 같이 구할 수 있습니다.
$$
p(\theta|\mathcal{D})=\frac{p(\mathcal{D}|\theta)p(\theta)}{p(\mathcal{D})}
$$
우리의 목표는 overfitting된 모델은 $p(\theta|\mathrm{D})$을 작게, 정확한 모델은 $p(\theta|\mathrm{D})$이 크게 나오게 만드는 것입니다. 여기서 $p(\mathcal{D})$는 바꿀 수 없고, $p(\mathcal{D}|\theta)$는 주어진 모델로 데이터를 예측하는 과정이기 때문에 모델을 바꾸지 않은 한 $p(\mathcal{D}|\theta)$을 계산하는 방법은 $p_\theta(y|x)p(x)$로 고정됩니다. 여기서 유일하게 바꿀 수 있는 것은 $p(\theta)$ 입니다.
우리는 $p(\theta)$, 또는 prior를 통해 overfitting된 모델을 피해야 합니다. 하지만 어떻게 $p(\theta)$를 통해 모델 학습에 영향을 줄수 있을까요? 이는 loss function을 $-\log p_\theta(y_i|x_i)$ 대신, $-\log p(\theta|\mathcal{D})$을 사용하면 됩니다.
$$
\begin{align}
\mathcal{L}(\theta)
&=-\log p(\mathcal{D}|\theta)-\log p(\theta)\\
&=-(\sum_i\log p_\theta(y_i|x_i))-\log p(\theta)
\end{align}
$$
여기서 $-\log p(\theta|\mathcal{D})$을 그대로 사용하지 않고 $p(\mathcal{D})$를 생략했습니다. 이는 $p(\mathcal{D})$가 항상 고정되어있기 때문에 굳이 계산할 필요가 없습니다. 그래서 바뀐 loss function을 보면 기존 loss function에서 $-\log p(\theta)$가 추가된 모습입니다.

이제 우리가 해야할 일이 명확해졌습니다. overfitting된 모델일 때는 $-\log p(\theta)$값을 높게, 좋은 모델은 낮게 나오도록 $p(\theta)$를 정해야 합니다. 이를 위해서 좋은 모델이 어떤 $\theta$값을 가지는지 가정해야 합니다.
여기서 사용할 가정은 절대값이 낮은 $\theta$일수록 정확히 예측한다는 것입니다. 파라미터 값의 절댓값이 크면 매우 복잡한 그래프를 그리기 때문에 overfitting될 수 있습니다. 하지만 절댓값이 매우 작다면 완만한 그래프를 그리기 때문에 모델이 그릴 수 있는 그래프보다 좀 더 단순한 모습을 가집니다.
절댓값이 낮은 $\theta$를 유도하기 위해 $p(\theta)=\mathcal{N}(0, \sigma^2)$으로 정할 겁니다. 그러면 $p(\theta)$는 다음과 같습니다.
$$
\begin{align}
\log p(\theta)&=\sum_i-\frac1{2\sigma^2}\theta_i^2-\log\sigma-\frac12\log 2\pi\\
&=-\lambda||\theta||^2+\mathrm{const}, \mathrm{where}\ \lambda=\frac1{2\sigma^2}
\end{align}
$$
위의 식에 따르면 $\theta$의 절댓값이 커지면 loss 값이 커집니다. 이를 loss function에 추가하면 optimizer를 통해 loss값을 낮추다보니 $\theta$는 낮은 절댓값으로 유도될 것입니다. 이런 Regularization을 L2 Regularization이라고 부릅니다.
또 다른 방법
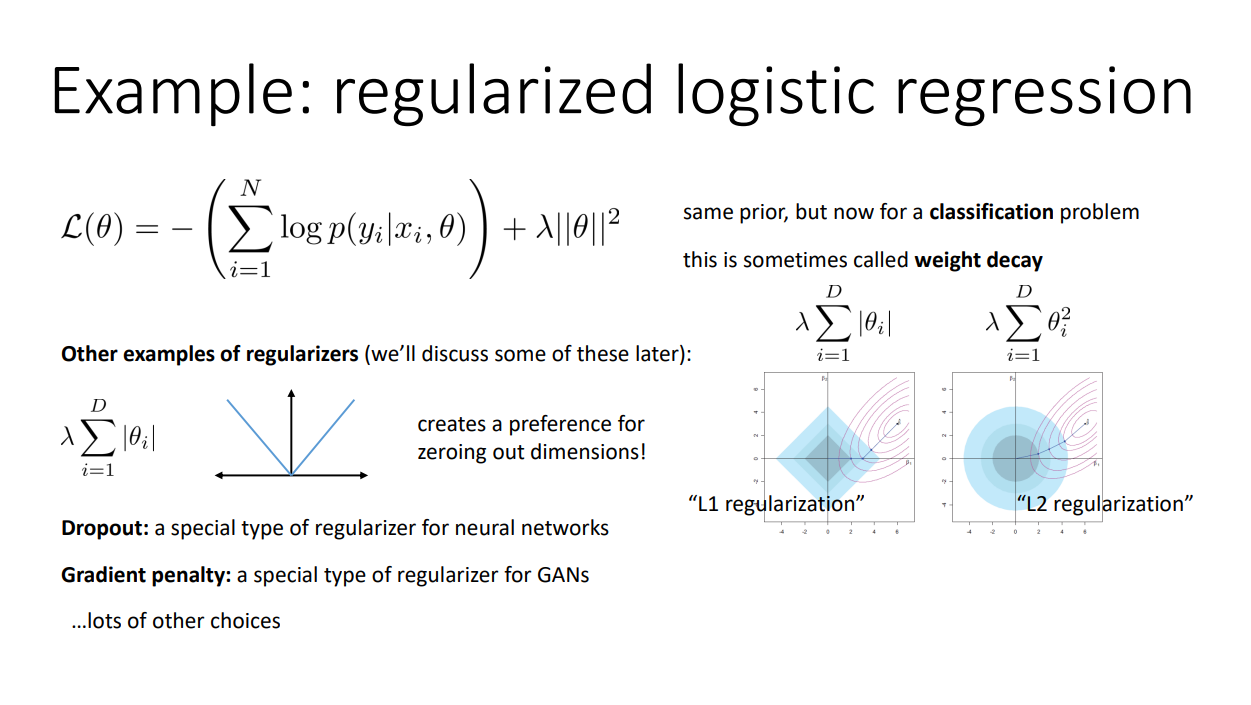
L2 Regularization만 존재하지 않습니다. L1 Regularization처럼 파라미터값의 제곱이 아닌 절댓값을 사용하는 방법, 일정 확률로 어떤 파라미터의 업데이트를 방해하는 Dropout, GAN처럼 서로 loss 값에 영향을 주는 Gradient penalty 등의 방법
Machine Learning Workflow
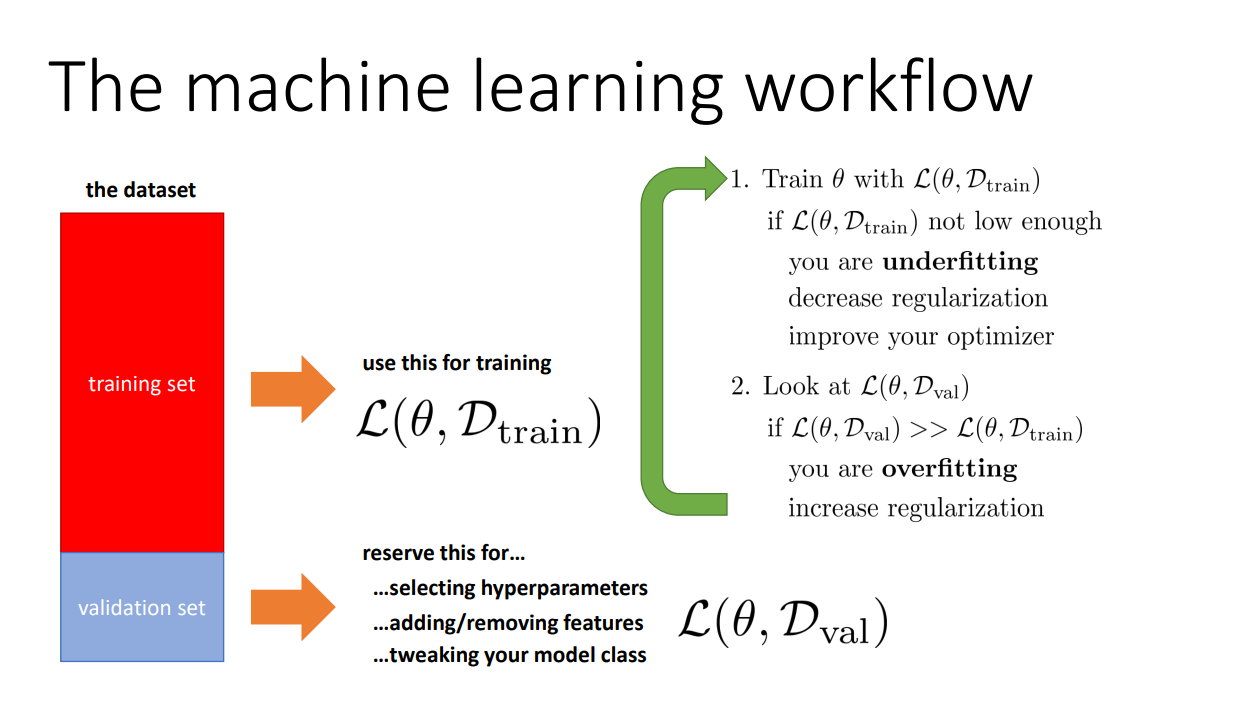
우리는 Variance와 Bias 모두 낮은 모델을 원합니다. 하지만 이를 단번에 찾기 어렵습니다. 그렇기 때문에 보통 다음과 같은 순서로 적절한 모델을 찾아냅니다.
- underfitting에서 벗어나기
- overfitting에서 벗어나기
- 찾은 모델의 최종 성능 평가하기
처음에는 학습 데이터셋 $\mathcal{D}_{\mathrm{train}}$을 학습합니다. 이때 $\mathcal{L}(\theta,\mathcal{D_\mathrm{train}})$값이 아직 높다면 모델의 복잡도를 높이고 regularization을 줄여 underfitting 상태에서 벗어납니다. 그 다음에는 검증 데이터셋 $\mathcal{D}_\mathrm{val}$으로 loss값 $\mathcal{L}(\theta,\mathcal{D}_\mathrm{val})$을 구합니다. 이때 $\mathcal{L}(\theta,\mathcal{D}_\mathrm{val})$값이 $\mathcal{L}(\theta,\mathcal{D}_\mathrm{train})$에 비해 높다면 regularization을 통해 overfitting에서 벗어납니다. 마지막으로 테스트 데이터셋을 통해 최종 모델의 성능을 확인합니다.
데이터셋 분리

보통 머신러닝 프로젝트에서 사용하는 데이터셋을 목적에 따라 학습용, 검증용, 테스트용 세가지로 분리합니다.
학습 데이터셋은 모델 학습에 사용되어 적절한 모델 파라미터값과 optimizer의 하이퍼파라미터 값을 찾습니다. 검증 데이터셋은 학습한 모델의 성능을 평가해 어떤 모델을 사용할지, 어떤 regularization 하이퍼파라미터 값을 쓸지 정하기 위해 사용합니다. 마지막으로 테스트 데이터셋은 앞의 과정에서 결정된 최종 모델의 성능을 평가하기 위해 사용합니다.
'인공지능 > CS182 스터디' 카테고리의 다른 글
| [CS182] Lecture 5: Backpropagation (0) | 2024.05.01 |
|---|---|
| [CS182] Lecture 4: Optimization (0) | 2024.04.10 |
| [CS182] Lecture 2: ML Basics 1 (머신러닝 문제의 종류, Model, Loss function, Optimizer) (0) | 2024.04.02 |
| [CS182] Lecture 1: Introduction (Representation과 Deep Learning이란) (0) | 2024.03.20 |
![[CS182] Lecture 3: ML Basics 2 (Bias-Variance Tradeoff, Regularization, Machine Learning Workflow)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbaGIsS%2FbtsGjliuNqh%2FKmnExRrGVNgyJjP7zoaOw0%2Fimg.png)